问题背景：如图1，四边形ABCD和CEFG都是正方形，B，C，E在同一条直线上，连接BG，DE．

问题背景：如图1，四边形ABCD和CEFG都是正方形，B，C，E在同一条直线上，连接BG，DE．
问题探究：
（1）①如图1所示，当G在CD边上时，猜想线段BG、DE的数量关系及所在直线的位置关系．（不要求证明）
②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，请选择图2或图3证明你的判断．
类比研究：
（2）若将原题中的“正方形”改为“矩形”（如图所示），且
AB
BC
=
CE
CG
=k（其中k＞0），请直接写出线段BG、DE的数量关系及位置关系．请选择图5或图6证明你的判断．
拓展应用：
（3）在（1）中图2中，连接DG、BE，若AB=3，EF=2，求BE 2 +DG 2 的值．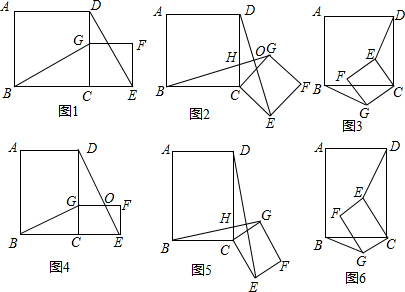
°高姿态 2020-06-26 悬赏5金币 已收到1个回答
赞

aiel722

共回答了65个问题采纳率：82.4%


解；（1）①BG=DE，BG⊥DE；
②仍然成立，选择图2证明如下：
证明：∵四边形ABCD、CEFG都是正方形；
∴BC=CD，CG=CE，∠BCD=∠ECG，
∴∠BCG=∠DCE，
∴△BCG≌△DCE（SAS），
∴BG=DE，∠CBG=∠CDE，
又∵∠BHC=∠DHO，∠CBG+∠BHC=90°，
∴∠CDE+∠DHO=90°，
∴∠DOH=90°，
∴BG⊥DE；

（2）BG⊥DE，
DE
BG =k，
如图5，


证明：
∵四边形ABCD，CEFG都是矩形，且
AB
BC =
EC
CG =k，
∴
DC
BC =
EC
CG =k，∠BCD=∠ECG=90°，
∴∠BCG=∠DCE，
∴△BCG ∽ △DCE，
∴∠CBG=∠CDE，
DE
BG =k，
又∵∠BHC=∠DHO，∠CBG+∠BHC=90°，
∴∠CDE+∠DHO=90°，
∴∠DOH=90°，
∴BG⊥DE；

（3）∵BG⊥DE，
∴BE 2 +DG 2 =OB 2 +OE 2 +OG 2 +OD 2 =BD 2 +GE 2 ，
又∵AB=3，CE=2，
∴BD=3
2 ，GE=2
2 ，
∴BD 2 +GE 2 =（3
2 ） 2 +（2
2 ） 2 =26，
∴BE 2 +DG 2 =26．
13
可能相似的问题

你能帮帮他们吗

精彩回答

Copyright © 2018 - 2026 XGT8.CN - 西瓜解题吧
西瓜单词 | 建筑试题 | 会计师试题
闽ICP备14005894号-7