题背景：如图1，四边形ABCD和CEFG都是正方形，B，C，E在同一条直线上，连接BG，DE．

题背景：如图1，四边形ABCD和CEFG都是正方形，B，C，E在同一条直线上，连接BG，DE．

问题探究：
小题1:（1）①如图1所示，当G在CD边上时，猜想线段BG、DE的数量关系及所在直线的位置关系．（不要求证明）
②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，请选择图2或图3证明你的判断．
类比研究：
小题2:（2）若将原题中的“正方形”改为“矩形”（如图所示），且 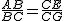=k（其中k＞0），请写出 线段BG、DE的数量关系及位置关系．请选择图5或图6证明你的判断（仅证数量关系）．
拓展应用：
小题3:（3）在（1）中图2中，连接DG、BE，若AB=3，EF=2，求BE 2 +DG 2 的值．
我非灯泡 2020-06-26 悬赏5金币 已收到1个回答
赞

stbz542

共回答了164个问题采纳率：92.3%

小题1:（1）①结论：ＢＧ＝ＤＥ　　ＢＧ⊥ＤＥ
② 结论:ＢＧ＝ＤＥ　　ＢＧ⊥ＤＥ　
证明(略)：
小题2:（2）结论： 　　　ＤＥ⊥ＢＧ
证明(略)：
小题3:（3）
　　　　　　　　
　　　　　　　　

略
19
可能相似的问题

你能帮帮他们吗

精彩回答

Copyright © 2018 - 2024 XGT8.CN - 西瓜解题吧
西瓜单词 | 建筑试题 | 会计师试题
闽ICP备14005894号-7