（2011•临川区模拟）问题背景：如图1，四边形ABCD和CEFG都是正方形，B，C，E在同一条直线上，连接BG，DE．

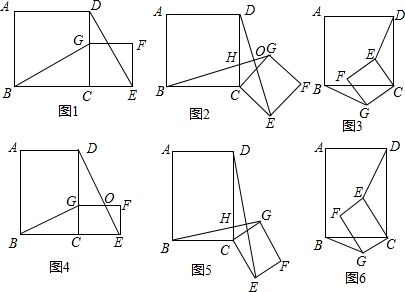（2011•临川区模拟）问题背景：如图1，四边形ABCD和CEFG都是正方形，B，C，E在同一条直线上，连接BG，DE．
问题探究：
（1）①如图1所示，当G在CD边上时，猜想线段BG、DE的数量关系及所在直线的位置关系．（不要求证明）
②将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2，如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，请选择图2或图3证明你的判断．
类比研究：
（2）若将原题中的“正方形”改为“矩形”（如图4所示），且[AB/BC＝
CE
CG]=k（其中k＞0），请直接写出线段BG、DE的数量关系及位置关系．请选择图5或图6证明你的判断．
拓展应用：
（3）在（1）中图2中，连接DG、BE，若AB=3，EF=2，求BE2+DG2的值．
四人疯 2020-06-26 悬赏10金币 已收到1个回答
赞

ABT453

共回答了111个问题采纳率：91.7%

解题思路：（1）①利用三角形全等的判定即可得出BG=DE，再利用对应角关系得出即可；
②利用三角形全等的判定即可得出BG=DE，再利用对应角关系得出即可；
（2）利用相似三角形的判定得出△BCG∽△DCE，进而得出即可；
（3）利用勾股定理得出BE2+DG2=OB2+OE2+OG2+OD2=BD2+GE2，进而得出答案即可．

解；（1）①BG=DE，BG⊥DE；
②仍然成立，选择图2证明如下：
证明：∵四边形ABCD、CEFG都是正方形；
∴BC=CD，CG=CE，∠BCD=∠ECG，
∴∠BCG=∠DCE，
∴△BCG≌△DCE（SAS），
∴BG=DE，∠CBG=∠CDE，
又∵∠BHC=∠DHO，∠CBG+∠BHC=90°，
∴∠CDE+∠DHO=90°，
∴∠DOH=90°，
∴BG⊥DE；

（2）BG⊥DE，[DE/BG]=k，
如图5，
证明：
∵四边形ABCD，CEFG都是矩形，且[AB/BC]=[EC/CG]=k，
∴[DC/BC]=[EC/CG]=k，∠BCD=∠ECG=90°，
∴∠BCG=∠DCE，
∴△BCG∽△DCE，
∴∠CBG=∠CDE，[DE/BG]=k，
又∵∠BHC=∠DHO，∠CBG+∠BHC=90°，
∴∠CDE+∠DHO=90°，
∴∠DOH=90°，
∴BG⊥DE；

（3）∵BG⊥DE，
∴BE2+DG2=OB2+OE2+OG2+OD2=BD2+GE2，
又∵AB=3，CE=2，
∴BD=3
2，GE=2
2，
∴BD2+GE2=（3
2）2+（2
2）2=26，
∴BE2+DG2=26．

点评：
本题考点： 相似三角形的判定与性质；勾股定理；矩形的性质；正方形的性质．

考点点评： 此题主要考查了全等三角形的判定以及相似三角形的判定与性质和勾股定理的应用，熟练利用相似三角形的性质得出是解题关键．

16
可能相似的问题

你能帮帮他们吗

精彩回答

Copyright © 2018 - 2024 XGT8.CN - 西瓜解题吧
西瓜单词 | 建筑试题 | 会计师试题
闽ICP备14005894号-7