已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB
| 已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD. (1)如图①,当PA的长度等于 时,∠PAB=60°;当PA的长度等于 时,△PAD是等腰三角形; (2)如图②,以AB边所在直线为x轴、AD边所在直线为y轴,建立如图所示的直角坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S 1 、S 2 、S 3 .坐标为(a,b),试求2 S 1 S 3 -S 2 2 的最大值,并求出此时a,b的值. 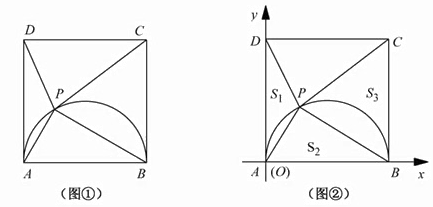 |
-
英语翻译XXX(人名),很抱歉的告诉你你的订单完成不了,中国新年快到了供货商和邮局都放假了,我这几天都没去拿货,不知道他
2024-08-147个回答
-
1295330000的近似数,近似数的有效数字( 精确到百分位 )科学计数法
2024-08-141个回答
-
求英语手工翻译: 首先很抱歉给你带来麻烦,这笔付款我已经让财务通知过Jason了,他应该会立即处理
2024-08-144个回答
-
2024-08-141个回答
-
2024-08-141个回答
-
把数38490按四舍五入精确法取近似值精确到千位是 ___ .
2024-08-141个回答
-
2024-08-141个回答
-
2024-08-141个回答
-
特别难的数学题1265330000精确到千万位,并用科学计数法表示为---------.这个近似数的有效数字有-----
2024-08-144个回答
-
2024-08-143个回答
-
2024-08-143个回答
-
2024-08-142个回答
-
4200万精确到百万位并用科学计数法表示 老师说答案是4.20*10^3万 ,问过程?我认为是4.2*10^3
2024-08-141个回答
-
把数精确到千位用科学计数法么?有一道题是这样的:把64497精确到千位可记为()A.6.4*10的四次方 B.64000
2024-08-142个回答
-
(20分)如图所示,A、B两个小物体(可看成质点)的质量分别为2m、m,它们栓接在跨过定滑轮的细绳两端,细绳不可伸长,且
2024-08-141个回答
-
不论m为何实数,直线(m-1)x-y+2m+1=0恒过定点( )
2024-08-141个回答
-
已知方程(3m-4)X的平方-(5-3m)x-4m=-2m是关于x的一元一次方程,(1)求m和x的值.
2024-08-141个回答
-
已知函数f(x)=x2-4x+a+3,g(x)=mx+5-2m.
2024-08-141个回答
-
2024-08-143个回答
-
解答这几题100分,要过程.一.1.24平方米=( )升=( )毫升二.把7分之2M分成8分,每分占总数的( )%,甲数
2024-08-145个回答
你能帮帮他们吗
-
初一寓言作文,600~400字的,最好不和别人重复.明天就交老师了.最好是动物的.
2024-08-141个回答
-
小学英语作文我最喜欢的动物是小兔子,它长着两只长耳朵,兔子喜欢吃萝卜,白菜,它蹦蹦跳跳很可爱,所以我很喜欢它.
2024-08-145个回答
-
2024-08-141个回答
-
2024-08-141个回答
-
2024-08-141个回答
精彩回答
-
1.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪只用),已建的仓库的底面直径为12米,高为4米,养路处拟建一
2024-08-142个回答
-
已知圆柱体钢罐(上下都有盖,封闭的)直径为12米,高9.4米,厚度为4厘米,.
2024-08-142个回答
-
2024-08-146个回答
-
知道圆柱高度和直径怎么算容积有一个圆柱体,高50厘米,直径是130CM,怎么计算出它里面有多少沙子,
2024-08-146个回答
-
2024-08-142个回答

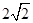 或
或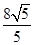 ;(2)当a=2时,b=2,2S 1 S 3 -S 2 2 有最大值是16.
;(2)当a=2时,b=2,2S 1 S 3 -S 2 2 有最大值是16.