1.某商店购进一批单价为16元的日用品,销售一段时间后,为了获得更多利润,商店决定提高销售价格.经实验发现,若按每件20
①试求y与x之间的关系式
②在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月最大利润是多少?
2.如图,在举行ABCD中AB=2,BC=1,以AB边所在的直线为x轴,AB的中点O为坐标原点建立平面直角坐标系,直线y=x+h(h>0)经过点D并与x轴,y轴分别交于点E、F.
①求h的值
②设反比例函数图像过点C,试确定它的表达式
③若抛物线经过E、F、B三点,求它的顶点坐标
上图图片画错
这个图是正确的
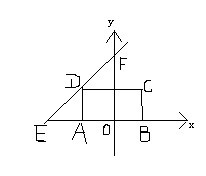
共回答了107个问题采纳率:100%
360=20k+b
210=25k+b
解得:k=-30,b=960
所以y=-30x+960((16≤x≤32).
②每月获得利润P=(-30x+960)(x-16)
=30(-x+32)(x-16)
=30(-x2+48x-512)
=-30(x-24)2+1920
所以当x=24时,P有最大值,最大值为1920.
答:当价格为24元时,才能使每月获得最大利润,最大利润为1920元.
2、①由题意知点D的坐标为(-1,1),代入y=x+h得
1=-1+h,h=2
②由题意知点C的坐标为(1,1)
因为反比例函数经过点C,所以设其表达式为y=k/x
将C点的坐标代入得1=k/1,k=1
所以反比例函数的表达式为y=1/x
③由题意知点B的坐标为(1,0)
由①知直线EF的表达式为y=x+2,分别令x=0,y=0,得y=2,x=-2
所以E(-2,0),F(0,2)
设所求抛物线的表达式为y=a(x+2)(x-1),将F(0,2)代入得
2=a(0+2)(0-1),a=-1
所以y=-(x+2)(x-1)=-(x2+x-2)=-(x+1/2)2+9/4
抛物线的顶点坐标为(-1/2,9/4)
-
2024-08-141个回答
-
悠悠球绳子长度和空转有关系吗?绳子长一点会不会让空转长一点?我就是怕短绳影响空转,也怕球老碰到地板,毕竟我才145多啊,
2024-08-141个回答
-
英语翻译RICHARD先生,很抱歉打扰到你.我不得已才这样做的.
2024-08-145个回答
-
关于悠悠球千机变千机变三种颜色,请问新手想买个练习1A的话买什么颜色的好,比如做双碟飞舞.翻天覆地之类动作的,还有空转如
2024-08-141个回答
-
英语翻译飞特,很抱歉今晚不能来找你玩了,因为我临时有急事,改约下次好吗?不需要逐字翻译,大致表达出这个意思就行.
2024-08-146个回答
-
请英语好的朋友帮助纠正一下翻译错误:“很抱歉听说你的这次考试没有通过,其实我也很紧张这次。。。”
2024-08-142个回答
-
英语简单翻译问题啊!老师、高手快来啊!纯自学菜鸟又不行了!谢谢
2024-08-141个回答
-
我们班同学上个周末玩的很愉快或我们度过了一个愉快的周末 英语句子翻译 快
2024-08-141个回答
-
英语翻译XXX(人名),很抱歉的告诉你你的订单完成不了,中国新年快到了供货商和邮局都放假了,我这几天都没去拿货,不知道他
2024-08-141个回答
-
英语翻译XXX(人名),很抱歉的告诉你你的订单完成不了,中国新年快到了供货商和邮局都放假了,我这几天都没去拿货,不知道他
2024-08-147个回答
-
1295330000的近似数,近似数的有效数字( 精确到百分位 )科学计数法
2024-08-141个回答
-
求英语手工翻译: 首先很抱歉给你带来麻烦,这笔付款我已经让财务通知过Jason了,他应该会立即处理
2024-08-144个回答
-
2024-08-141个回答
-
2024-08-141个回答
-
把数38490按四舍五入精确法取近似值精确到千位是 ___ .
2024-08-141个回答
-
2024-08-141个回答
-
2024-08-141个回答
-
特别难的数学题1265330000精确到千万位,并用科学计数法表示为---------.这个近似数的有效数字有-----
2024-08-144个回答
-
2024-08-143个回答
-
2024-08-143个回答
你能帮帮他们吗
-
2024-08-141个回答
-
2024-08-141个回答
-
2024-08-141个回答
-
2024-08-143个回答
-
已知m是正整数,函数f(x)=(2m-m^2)x^2m^+3m-4在(0,∝)上是增函数. (1)求f(x)的解析式.
2024-08-141个回答
精彩回答
-
圆柱形油桶的底面直径4米,高50厘米,做五个这样的铁皮油桶至少需要多少平方分米的铁皮?
2024-08-142个回答
-
喷泉的直径是12米,高是0.4米,问问这个喷泉的占地面积是多少
2024-08-142个回答
-
英语语法How time_____!A.flyingB.flyC.fliesD.is flying是一封信的第一句话
2024-08-144个回答
-
1.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪只用),已建的仓库的底面直径为12米,高为4米,养路处拟建一
2024-08-142个回答
-
已知圆柱体钢罐(上下都有盖,封闭的)直径为12米,高9.4米,厚度为4厘米,.
2024-08-142个回答
