初二数学几何已知如图,在△ABC中,AD垂直BC,垂足为点D,BE垂直AC,垂足为E,M为AB边上的中点,连结ME,MD

初二数学几何

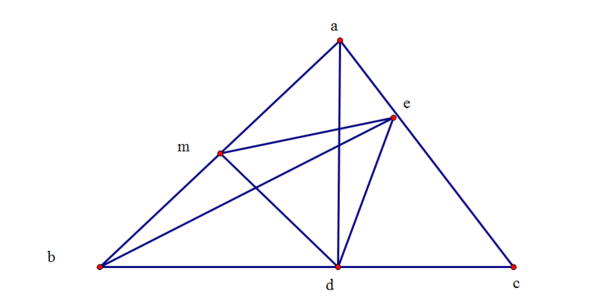
已知如图,在△ABC中,AD垂直BC,垂足为点D,BE垂直AC,垂足为E,M为AB边上的中点,连结ME,MD,ED,且三角形MED为等腰三角形,

求证：∠EMD=2∠DAC

不雨花犹落 2024-04-29 悬赏16金币 已收到2个回答
赞

赤乌

共回答了95个问题采纳率：80%

由直角三角形斜边中线等于斜边的一半,
可知DM=ME=BM=AM
从而还知角DMB=2倍角BAD,角AME=2倍角ABC
则角DMB+角AME+角DME=180度=2倍角BAD+2倍角ABC+2倍角EBC
得角EMD=2倍角EBC
而角EBC=角DAC（同角的余角相等）
即角EMD=2角DAC
13

yanjiaya0827

共回答了105个问题

你好　
证明：（1）∵M为AB边的中点，AD⊥BC， BE⊥AC，
∴ MD=ME=MA=MB(斜边上的中线=斜边的一半）
∴△MED为等腰三角形
（2）∵ME=MA ∴∠MAE=∠MEA
∴∠BME=2∠MAE
∵MD=MA ∴∠MAD=∠MDA...
7
可能相似的问题

你能帮帮他们吗

精彩回答

Copyright © 2018 - 2024 XGT8.CN - 西瓜解题吧
西瓜单词 | 建筑试题 | 会计师试题
闽ICP备14005894号-7